1. 점근적 실행 시간 = 시간 복잡도
점근적 실행 시간은 시간복잡도라 할 수 있고 시간복잡도의 정의는 어떤 알고리즘을 수행하는 데 걸리는 시간을 설명하는 계산 복잡도를 이야기 한다.
계산 복잡도를 표기하는 대표적인 방법이 바로 빅-오 이다.
2. 빅오는 점근 표기법(asymptotic notation)의 한 종류
점근 표기법은 어떤 함수의 증가 양상을 다른 함수와의 비교로 표현하는 수론과 해석학의 방법이다. 알고리즘의 복잡도를 단순화할 때나 무한급수의 뒷부분을 간소화할 때 쓰인다.
점근 표기법에는 빅-오, 빅-세타, 빅-오메가, 리틀-오, 리틀-오메가 가 있다.
1. 빅-오(big-o) : 상한을 의미 한다.
2. 빅-오메가 : 하한을 의미한다.
3. 빅-세타 : 평균을 의미한다.

(출처 : 위키피디아:(https://ko.wikipedia.org/wiki/%EC%A0%90%EA%B7%BC_%ED%91%9C%EA%B8%B0%EB%B2%95))
3. 빅오(big-o)
- 입력 값이 무한대로 향할때 함수의 상한을 설명하는 수학적 표기 방법
- 실행 시간(시간복잡도)와 공간 요구사항(공간 복잡도)가 어떻게 증가하는지를 분류
- 알고리즘의 효율성을 분석 하는데 사용
빅오로 시간복잡도를 표기할 때 최고차항만을 표기, 상수항은 무시
- 최고차항 무시 : 5n^2 + 3n + 4 을 시간 복잡도는 5n^2 만을 고려한다.
- 상수항은 무시 : O(5n^2) ▶ O(n^2)
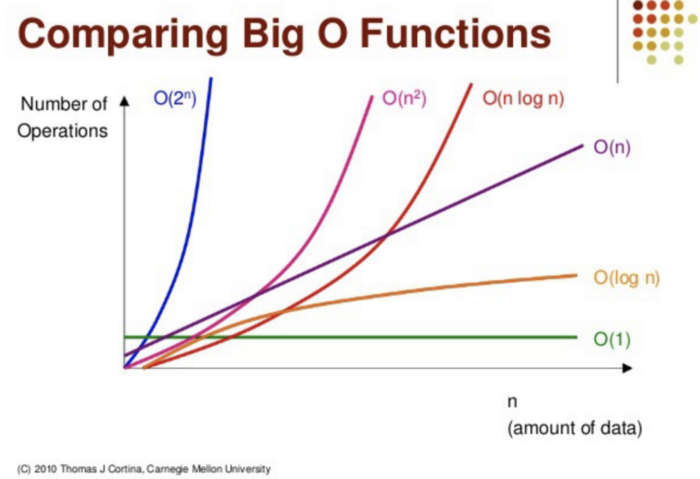
4. 빅오의 표기법
- O(1) : 입력 값이 아무리 커도 실행 시간은 일정하다.
- 예) 해시 테이블의 조회 및 삽입
- O(log n) : 입력값에 영향을 받지만 크게 받지 않는다. n의 크기에 매우 견고하다
- 예) 이진 검색
- O(n) : 알고리즘을 수행하는 데 걸리는 시간은 입력값에 비례한다. 선형 시간 알고리즘이라고 한다.
- 예) 정렬되지 않은 리스트에서 최댓값 또는 최솟값 찾는 경우
- O(n log n) : 병합 정렬을 비록한 대부분의 효율 좋은 정렬 알고리즘이 이에 해당한다. 적어도 한 번 이상은 비교해야 하는 비교 기반 정렬 알고리즘은 아무리 좋은 알고리즘도 O(n log n)보다 빠를 수 없다.
- O(n^2) : 버블 정렬 같은 비효율적인 정렬 알고리즘이 이에 해당한다.
- O(2^n) : 피보나치 수를 재귀로 계산하는 알고리즘이 이에 해당한다.
- O(n!) : 가장 느린 알고리즘으로, 입력값이 조금만 커져도 웬만한 다항시간 내에는 계산이 어렵다.
- 예) 각 도시를 방문하고 돌아오는 가장 짧은 경로를 찾는 외판원 문제를 브루트 포스로 풀이할 때가 이에 해당
빅오는 최악을 나타내는 것이 아니라, 빅오 표기법은 주어진(최선/최악/평균) 경우의 수행 시간의 상한을 나타낸다.
참고자료 :파이썬 알고리즘 인터뷰 (박상길 지음, 정진호 일러스트)
'알고리즘' 카테고리의 다른 글
| 요소 개수 찾기 count() , Counter (1) | 2022.10.07 |
|---|---|
| 정렬(오름,내림 차순) 및 리스트 요소 순서 뒤집기(reverse,reversed) (0) | 2022.10.05 |
| 프로그래머스 - Lv1. 두 정수 사이의 합 (0) | 2022.10.03 |
| 프로그래머스 - Lv1. 정수 제곱근 판별 (0) | 2022.10.03 |
| 진수 변환 (0) | 2022.03.15 |
